GRBM Efficiency with Direction

The same work has been repeated by taking into account the incoming direction of every BATSE burst, as referred to the GRBM local frame of reference; therefore, the local sky has been split according to two different regular grids: first, into six different parts of equal area, each facing one of the six faces of the GRBM box (the four GRBM units, disposed as lateral shields around the PDS, and the local north and south as well), and the common sample of GRBM & BATSE GRBs has been divided into the six corresponding classes, depending on the local arrival directions. After doing the same for the sample of BATSE GRBs that should have been detected, it has been possible to estimate the above GRBM efficiency as a function of the GRB arrival direction. The GRBM local sky has been split into six regions, like the faces of a cube. Second, the same operations have been repeated also by adopting a dodecahedron grid, instead of a cube grid; on one hand, this grid is finer, while on the other hand, it has a little worse statistical quality, since each region includes a smaller number of bursts than in the cube case.

A given direction is considered to belong to the $n$-th face, whenever the mininum angular distance between the given direction and the normal direction to the $i$-th face ($i=1,\ldots,6$ or 12, depending on whether the cube or the dodecahedron grid is considered, respectively), occurs when $i=n$. In the case of the cube grid, the six cube faces, corresponding to the six sky regions, are so numbered: face # 1 corresponds to GRBM unit 1, and so on till # 4 facing GRBM 4; then face # 5 refers to the top face (pointing along the same direction of the NFIs), while # 6 faces the opposite direction, i.e. the BeppoSAX local south pole. For the dodecahedron faces, their local coordinates can be read from table .

In the following table  the results are reported in two cases: first, by taking into account only the BATSE 4B catalog; second, the three merged catalogs: BATSE 4B, Kommers' and Stern's (4B+K+S, in the table). Both the cube and the dodecahedron grid cases are reported; in the latter case, only the merged catalogs have been considered, otherwise the statistics would be poor.

Table: GRBM off-line efficiency as a function of the local direction, according to a cube grid (top table), and to a dodecahedron grid (bottom table).

Local Sky	$\phi$	$\theta$	Det	Exp	$\epsilon_{\mbox{\small {off}}}$	Det	Exp	$\epsilon_{\mbox{\small {off}}}$
Region	($\rm ^{\circ}$)	($\rm ^{\circ}$)	(4B)	(4B)	(4B)	(4B+K+S)	(4B+K+S)	(4B+K+S)
(Cube)
GRBM 1	270	0	55	65	$0.85 \pm 0.11$	75	112	$0.67 \pm 0.08$
GRBM 2	0	0	59	75	$0.79 \pm 0.10$	75	129	$0.58 \pm 0.07$
GRBM 3	90	0	43	58	$0.74 \pm 0.11$	62	103	$0.60 \pm 0.08$
GRBM 4	180	0	34	51	$0.67 \pm 0.11$	43	92	$0.47 \pm 0.07$
North Pole	0	+90	43	55	$0.78 \pm 0.12$	52	94	$0.55 \pm 0.08$
South Pole	0	-90	28	84	$0.33 \pm 0.06$	32	132	$0.24 \pm 0.04$
Total	-	-	262	388	$0.67 \pm 0.04$	339	662	$0.51 \pm 0.03$

Local Sky	$\phi$	$\theta$	Det	Exp	$\epsilon_{\mbox{\small {off}}}$
Region	($\rm ^{\circ}$)	($\rm ^{\circ}$)	(4B+K+S)	(4B+K+S)	(4B+K+S)
(Dodecahedron)
Face 1	0	+90.00	24	48	$0.50 \pm 0.10$
Face 2	90	+26.56	25	46	$0.54 \pm 0.11$
Face 3	162	+26.56	26	45	$0.58 \pm 0.11$
Face 4	234	+26.56	32	52	$0.62 \pm 0.11$
Face 5	306	+26.56	54	68	$0.79 \pm 0.11$
Face 6	18	+26.56	36	52	$0.69 \pm 0.12$
Face 7	0	-90.00	17	67	$0.25 \pm 0.06$
Face 8	270	-26.56	28	64	$0.44 \pm 0.08$
Face 9	342	-26.56	26	60	$0.43 \pm 0.08$
Face 10	54	-26.56	33	59	$0.56 \pm 0.10$
Face 11	126	-26.56	26	51	$0.51 \pm 0.10$
Face 12	198	-26.56	12	50	$0.24 \pm 0.07$
Total	-	-	339	662	$0.51 \pm 0.03$

Figure: GRBM off-line efficiency as a function of the local direction (aitoff projection); these values have been obtained by splitting the local sky according to two regular grids: cube- and dodecahedron-shaped; then, the results have been merged into a unique figure.

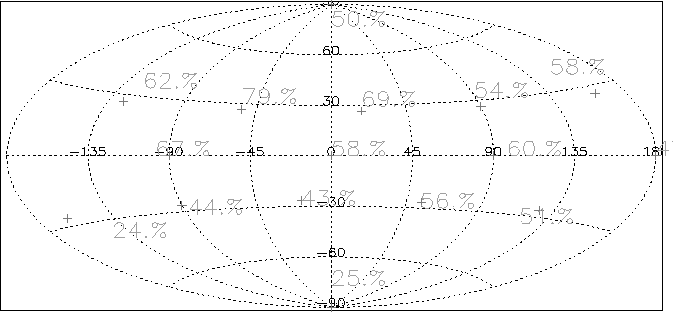The results reported in table  suggest some observations: the GRBM efficiency looks quite constant within the uncertainties, except for the BeppoSAX local south pole, where it falls down to $\sim$33% for BATSE 4B bursts only ($\sim$24-25%, including the non-triggered bursts), with a significant decrease with respect to the other local directions. This is explained with the presence of the on-board electronics boxes in the lower part of the spacecraft, in agreement with the Monte Carlo simulations (fig. ). The average efficiency is $\sim(75 \pm 10)$% for the directions facing the four GRBM units and the north pole (the NFI pole), although there is a mild indication that the GRBM unit # 1 has a little better efficiency than the others, likewise the GRBM unit # 4 looks a little worse, though not significatively.

Finally, one might note that the number of BATSE 4B common bursts (262) reported in table  and the number of total bursts, including the BATSE non-triggered catalogs (339), are smaller than the corresponding numbers 283 and 283+79=362, respectively, reported in tables  and : actually, some bursts happened when the BeppoSAX spacecraft attitude was not known, during the time interval May - July 1997; hence, for these GRBs, the transformation from celestial to local coordinates was not feasible; owing to this, they have not been taken into account for estimating the GRBM efficiency as a function of the local direction.