
Edward Rapkin, Ph.D.
IN/US Systems, Inc.
Photomultiplier tubes (PMTs) are at the heart of radioisotope detectors used in bio-medical research. Commercial liquid scintillation counters and flow-through systems have two of them, most gamma counters have one. Still, the numbers involved have never been large enough to enable the nuclear instrument manufacturer to call the tune. We take what the PMT manufacturer offers and do our best with what is available; we accommodate to the PMTs and not the other way around. The PMTs help define the manner in which measurements are made. If nothing else, an understanding of the workings of the PMT should provide intellectual satisfaction to those who use them so extensively.
PMTs are, of course, detectors of light, not of radioactivity. In contrast to Geiger and proportional counters and solid state detectors which are directly responsive to radioactive decay, PMTs are not (other than for some secondary and unwanted effects). Rather, there is a primary detector, a scintillator; either in solution or a solid (which may be particulate or a massive crystal), its light output in response to radioactive decay is then measured with the PMT.
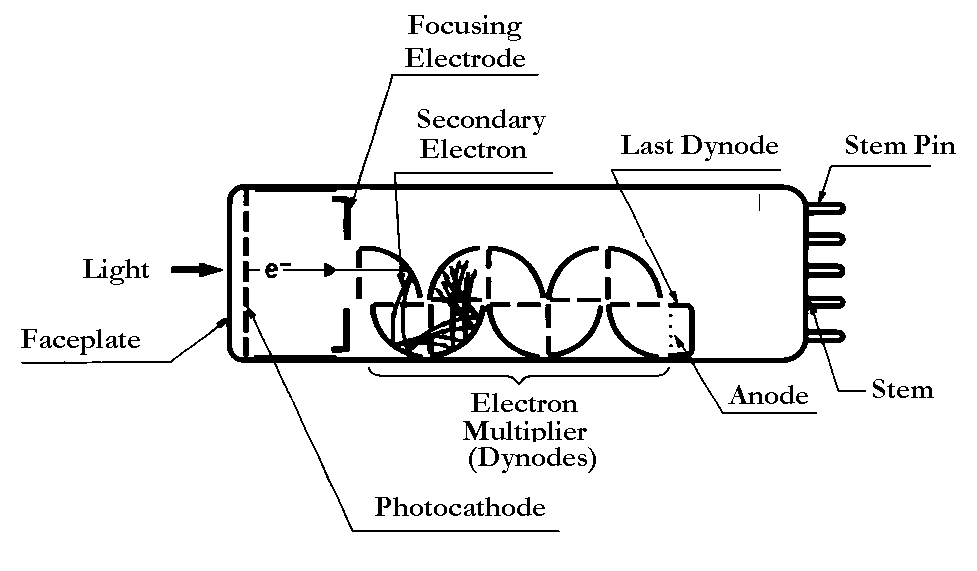
PMTs are very special vacuum tubes. Those used in nuclear instrumentation are "end-on", sometimes called "head-on". Constructed of glass or quartz tubing, at one end there is a flat or hemispherical faceplate on whose inner surface has been deposited the semi-transparent photocathode, a light-sensitive electron-emissive film containing antimony together with one or more alkali metals -- Na, K, Cs, Rb. The other end, the base, supports the internal dynode string, 10-12 metal plates, which sequentially multiply the number of electrons (often termed "photoelectrons") released by the photocathode under light stimulus. The last element in the chain is the anode, the receptor for electrons streaming off the last dynode.
Each dynode, the photocathode, the anode, and often a focus electrode preceding the first dynode, are separated by insulators and are independent of one another; connections to individual pins in the base bring operating voltages to each of the elements. The "bleeder string" at the PMT socket divides up the high voltage between the photocathode and first dynode, between each subsequent pair of dynodes, and between the last dynode and the anode.
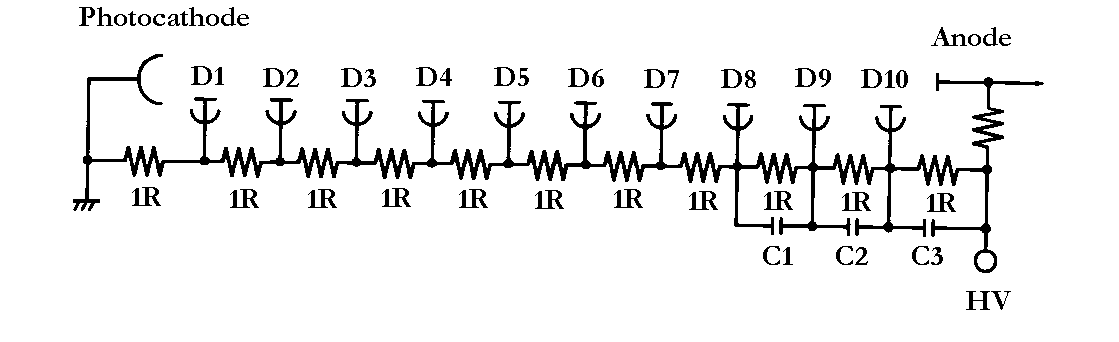
The bleeder consists of a series of high value (to limit current flow) resistors, often soldered directly to the pins of the PMT socket; frequently all have the same resistance though, to improve collection efficiency at the first stages where relatively few electrons are flowing, a greater resistance is sometimes employed to obtain a greater voltage differential. A simplified bleeder string is illustrated in Fig. 1. It represents a PMT with 10 dynodes and there are 11 resistors in the string, all with the same value. With 1100 volts applied across the entire string, there is a voltage drop of 100 volts between each successive element. However, if the first resistor (between the photocathode and the first dynode) has a resistance of 3R, and the second resistor a value of 2R, then the 1100 volts is divided 14 ways and the first drop will be 236 volts, the next 157 volts, and all the remaining 79 volts.
To understand why it matters we should look at the PMT itself. Several dynode structures are currently used; Fig. 2 illustrates one of them -- "box and grid" -- discussed because of its simplicity. The dynodes are quarter cylinders whose inside surface has been treated to have a low "work function", i.e., the ability to release multiple electrons when struck by a single electron. Facing each dynode and electrically connected to it, a fine wire mesh grid creates a field to attract and accelerate electrons leaving the preceding stage. Since the dynode and the grid are at the same potential and the grid is largely open, most of the electrons pass through and strike the dynode resulting in secondary-emission multiplication.
The degree of multiplication is a function of the interdynodal potentials which accelerate the electron beam; it is typically from 3 to 8 per stage or, overall, 106 to 107. System stability is very much dependent upon high voltage stability; anode output varies directly with the 6th to 10th power of any change in applied voltage.
Proper high voltage is critical to obtaining acceptable counting performance. Electronic amplifiers that necessarily follow the PMTs have inherent noise levels. If the H.V is insufficient, the PMT output is too small for subsequent amplification; the signal is lost in the noise. But, if the H.V. is excessive, the anode dark current, a small current that flows in a PMT in the complete absence of light, increases exponentially and masks the signal. Dark current derives from a combination of several sources.
Thermionic electrons, from the photocathode and first few dynodes released at room temperature due to their very low work functions, are multiplied up the dynode chain; electrons from the later dynodes are less a problem as they are not subject to as much multiplication. This effect limits the useful voltage drops in the early stages and 2R and 1.2R are more usual than the 3R and 2R cited in the example above.
Ion feedback is a sometime result of the collision of residual gases in the tube with electrons causing ionization. Should some of these ions drift to the photocathode and early dynodes, secondary electrons may be released which after multiplication down the chain result in relatively large noise pulses. These pulses are seen as afterpulses which quickly follow the primary signal by a time related to ionic drift. At low count rates, they can be distinguished from the primary pulses by fast circuitry and suppressed by imposing artificial dead time or other electronic means.
Glass scintillation is the most significant problem of PMTs used for low-level counting. Extraneous light poses the risk of finding its way to the photocathode and releasing photoelectrons which are multiplied down the dynode string; since the photocathode is "semi-transparent", photons from one PMT of a coincidence system occasionally activate both ("photomultiplier crosstalk"). One source of these photons is electrons which deviate from their normal trajectories and strike the glass envelope. Still another is Cerenkov light resulting from the decay of K-40 and other radioactive isotopes naturally present in glass. A lesser source, the interaction of cosmic rays and ambient activity with the glass, has more or less the same effect.
The obvious solutions are to both minimize the size of the PMT, thereby minimizing glass, and to operate at relatively low H.V. so as not to amplify small events to the point where they are counted. The latter may not always be possible, especially for H-3 measurement where one begins with few photons; for more energetic isotopes, operating at decreased high voltage is an attractive possibility. And, reduced high voltage minimizes still another problem -- field emission; the dynodes of PMTs operated near their maximum voltage may spontaneously emit electrons due to strong electric fields, which electrons lead to noise and spurious counts.
Finally, we briefly address two topics intimately related to our PMTs -- photocathode sensitivity and coincidence counting. The photocathode, whose composition has been largely determined by the need for a low work function, is most responsive between 350 and 450 nanometers with a peak response (about 25% quantum efficiency) at 420 nm. Scintillators must be chosen for maximum light output in that region and solvent systems for maximum transparency; similarly, solid scintillators and sample containers or flow-cell tubing must be equally transparent.
For low-energy beta- and gamma-emitters the scintillation process produces few photons; PMT output pulses may be no larger than PMT noise pulses. With noise rates typically 3,000-30,000 pulses per minute at the high voltage necessary for maximum H-3 efficiency, useful counting with a single PMT is limited to rather high activity samples. However, if two PMTs look at the same radioactive sample and the requirement is made that a count can only be recorded when both PMTs output within a "coincidence time" of 20-50 nanoseconds, and with noise pulses typically only about 10 nanoseconds wide, then legitimate decay events, true background, and photomultiplier crosstalk are counted. Very little of the noise from one PM coincides with noise from the other; perhaps 1 "accidental" count per minute or less finds its way into the totals.
Coincidence counting is not without its drawbacks. On average, the number of photons incident on each PM is halved. For the lowest energy events the number of photons falling on each photocathode is insufficient to release photoelectrons from both and no count is recorded. All other events produce smaller pulses than would be the case with all photons falling on one PM. Signal amplitude is reduced, thereby requiring still higher voltages resulting in increased noise. Nevertheless, the overall result is salutary; perhaps counting efficiency is reduced a few percent but the decrease in noise as it might contribute to observed background is surely in the area of 99.99 %.
