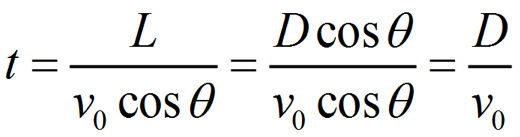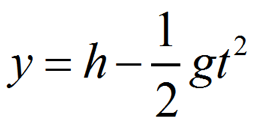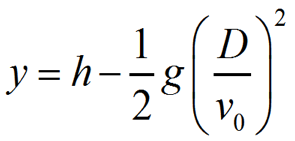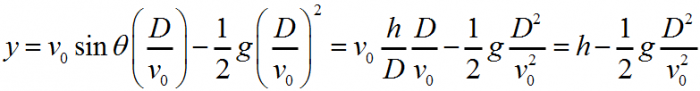Il Dilemma della scimmia.

Un cannone “sparabanane” è puntato su una scimmia che si sta dondolando su una liana. Nello stesso identico momento in cui il cannone spara la banana la scimmia si lascia cadere. Il punto è: la scimmia mangerà la banana?

Supponiamo che l'altezza della scimmia sia h, la distanza orizzontale dal del cannone dalla scimmia sia L e la distanza effettiva tra cannone e scimmia sulla liana sia D.

Dalla formula del moto rettilineo uniforme, ricaviamo il tempo che la banana impiega a percorrere la distanza L in orizzontale tramite il rapporto tra spazio e velocità orizzontale v_0x = v₀ · cosθ :

A questo punto bisogna controllare a che quota si trovino la scimmia e la banana nell'istante t in cui questa raggiunge orizzontalmente la distanza L. Il moto della scimmia che cade è un moto uniformemente accelerato, con accelerazione di gravità. La legge oraria del moto sarà:

con h per y₀ e velocità iniziale pari a zero perché parte da ferma. Quando la banana si trova a distanza L dal punto di partenza, la scimmia si troverà nella posizione definita dall'istante di tempo trovato prima, e cioè:

Consideriamo ora la quota della banana. Essendo anche il suo un moto uniformemente accelerato lungo la verticale, sostituiamo nell'equazione il tempo e la componente verticale della velocità v_0y = v₀· sinθ :

Quindi le traiettorie della scimmia e della banana si intersecano allo stesso istante e la scimmia mangerà la banana.

Di seguito il link dell'esperimento reale compiuto al MIT di Boston:

https://www.youtube.com/watch?v=cxvsHNRXLjw